Viewing entries in
Quantum Mechanics

Schrödinger's lunch

While visiting the University of Vienna for a conference, I came across Erwin Schrödinger's old desk set up in the lunch room. Sitting down at the desk to eat my lunch I stumbled upon a new quantum "paradox". Schrodinger's lunch

The blackhole firewall paradox

Excellent overview by Jennifer Ouellette of a new paradox that is taking the physics world by fire. I first heard about this a month ago from Patrick Hayden. It looks like this could turn into one of the great thought experiments that tackles the difficulties merging quantum mechanics and general relativity.

Paradoxes in physics have a way of clarifying key issues. At the heart of this particular puzzle lies a conflict between three fundamental postulates beloved by many physicists. The first, based on the equivalence principle of general relativity, leads to the No Drama scenario: Because Alice is in free fall as she crosses the horizon, and there is no difference between free fall and inertial motion, she shouldn’t feel extreme effects of gravity. The second postulate is unitarity, the assumption, in keeping with a fundamental tenet of quantum mechanics, that information that falls into a black hole is not irretrievably lost. Lastly, there is what might be best described as “normality,” namely, that physics works as expected far away from a black hole even if it breaks down at some point within the black hole — either at the singularity or at the event horizon.

Together, these concepts make up what Bousso ruefully calls “the menu from hell.” To resolve the paradox, one of the three must be sacrificed, and nobody can agree on which one should get the ax.

Physicists don’t lightly abandon time-honored postulates. That’s why so many find the notion of a wall of fire downright noxious. “It is odious,” John Preskill of the California Institute of Technology declared earlier this month at an informal workshop organized by Stanford University’s Leonard Susskind. For two days, 50 or so physicists engaged in a spirited brainstorming session, tossing out all manner of crazy ideas to try to resolve the paradox, punctuated by the rapid-fire tap-tap-tap of equations being scrawled on a blackboard. But despite the collective angst, even the firewall’s fiercest detractors have yet to find a satisfactory solution to the conundrum.

Joe Polchinski, one of the authors who published the paper on the blackhole firewall paradox, has a more technical write up of the subject over on Cosmic Variance.

Earlier this year, with my students Ahmed Almheiri and Jamie Sully, we set out to sharpen the meaning of black hole complementarity, starting with some simple `bit models’ of black holes that had been developed by Samir Mathur and Steve Giddings. But we quickly found a problem. Susskind had nicely laid out a set of postulates, and we were finding that they could not all be true at once. The postulates are (a) Purity: the black hole information is carried out by the Hawking radiation, (b) Effective Field Theory (EFT): semiclassical gravity is valid outside the horizon, and (c) No Drama: an observer falling into the black hole sees no high energy particles at the horizon. EFT and No Drama are based on the fact that the spacetime curvature is small near and outside the horizon, so there is no way that strong quantum gravity effects should occur. Postulate (b) also has another implication, that the external observer interprets the information as being radiated from an effective membrane at (or microscopically close to) the horizon. This fits with earlier observations that the horizon has effective dynamical properties like viscosity and conductivity.

I love that one of the postulates is called "no drama."

New arxiv.org paper: Detection loophole closed using photons

A new paper just appeared on the arxiv that claims to close the detection loophole (also known as the fair-sampling loophole) in Bell's Inequalities. If this is true (and from a first reading it appears they have a solid case) it is another important step along the way to a loophole free test of Bell's inequalities. This makes photons the first system in which all loopholes have been closed independently. Now the (even more) difficult task of a loophole free experiment begins.

Once the paper goes through the peer review process I will try and post a more detailed write up about the results. In the meantime, grab the preprint from the arxiv. Congratulations to all those involved!

Here is the abstract:

The violation of a Bell inequality is an experimental observation that forces one to abandon a local realistic worldview, namely, one in which physical properties are (probabilistically) defined prior to and independent of measurement and no physical influence can propagate faster than the speed of light. All such experimental violations require additional assumptions depending on their specific construction making them vulnerable to so-called "loopholes." Here, we use photons and high-efficiency superconducting detectors to violate a Bell inequality closing the fair-sampling loophole, i.e. without assuming that the sample of measured photons accurately represents the entire ensemble. Additionally, we demonstrate that our setup can realize one-sided device-independent quantum key distribution on both sides. This represents a significant advance relevant to both fundamental tests and promising quantum applications.

Entangling three photons in energy and time

Entangling three photons in energy and time

Our latest paper, on which I was the lead author, has just been published in Nature Physics. I am working with Jasper Palfree to develop a comprehensive page that explains the work. Unfortunately, that is not ready yet. In the mean time, here is the official press release:

Photon Triplet Counts

Extending Einstein

Researchers at the University of Waterloo and the University of Calgary have carried out an experiment, using the quantum properties of three particles light, that could provide new insights into the philosophical arguments by Einstein about the foundations of quantum mechanics.

In 1935 Albert Einstein, Boris Podolsky, and Nathan Rosen (EPR) published a thought experiment designed to show that quantum mechanics, by itself, is not sufficient to describe reality. Using two entangled particles – particles that share correlations stronger than those allowed by classical physics – EPR tried to demonstrate that there must be some hidden parameters that quantum mechanics does not account for. The ensuing debate led to the pioneering work of John Bell who, in 1964, showed that by following the arguments of EPR to their logical conclusion one arrives at a contradiction with experiments; hidden parameters, like the ones EPR argued for, are incompatible with our observations of nature and the mystery at the heart of quantum mechanics remains intact. This has profoundly shaped our understanding of quantum theory, and today the entanglement between two particles that EPR first proposed is a valuable resource in emerging quantum technologies like quantum computing, quantum cryptography, and quantum precision measurements.

77 years after EPR's landmark work a new paper in Nature Physics, authored by physicists at the Institute for Quantum Computing in Waterloo and at the University of Calgary, has finally experimentally extended the original ideas of Einstein and his colleagues from two to three entangled particles. This new form of three-particle entanglement, based on the position and momentum properties of photons, may prove to be a valuable part of future communications networks that operate on the rules of quantum mechanics, and could lead to new fundamental tests of quantum theory that deepen our understanding of the world around us. According to group leader Thomas Jennewein, "It is exciting, after all this time, to be able to create, control, and entangle quantum particles in this new way. Using these states of light it may be possible to interact with and entangle distant quantum computer memories based on exotic atomic gases."

In the experiment the researchers took a highly energetic blue photon and passed it through a special crystal that caused it to split into a pair of red coloured daughter photons. They then repeated this process with one of the daughter photons to create three entangled photons. The energy of these three photons, through the conservation of energy, must be equal to the energy of the original blue photon. Because the splitting process is instantaneous, the three photons must arrive at the detectors at the same time. It is therefore possible to learn the precise energy (corresponding to their total momentum) of the three photons as well as their arrival times (corresponding to their position). At first this seems to be an apparent contraction with the Heisenberg uncertainty principle which states that it is impossible to simultaneously learn arbitrarily precise information about a particle's position and momentum. However, with entangled particles, it is possible to gain precise information about the sum and differences of their position and momentum in a manner not possible with classical particles. This is in part because each of the particles in an entangled state gives up its own individual identity–the properties of the particles are instead shared collectively. It still remains impossible to gain position and momentum information of any individual particle. Says lead author Krister Shalm, "It is as if you could only discover how many points two teams combined to score in a basketball game, but had no way of knowing how many points each individual team had scored." Co-author Deny Hamel adds, "Because the entangled photons cooperate with one another they can do things that classical particles are unable to."

The next step for the researchers is to try to combine the position and momentum entanglement between their three photons with more traditional types of entanglement based on angular momentum. This will allow the creation of hybrid quantum systems that combine multiple unique properties of light at the same time. According to Christoph Simon from the University of Calgary, "This work opens up a rich area of exploration that combines philosophy, quantum mechanics, and quantum technologies. The powerful insights by Einstein and his co-workers in 1935 are still informing the way we understand the world around us."

The CIA and Jeff Bezos Bet on Quantum Computing

A 30 million dollar bet. That's a lot of money for D-Wave.

It's an attitude that seems to have played well with investors, but it still rankles academics. "At an engineering level they've put together a setup that's impressive in various ways," says Scott Aaronson, an MIT professor who studies the limits of quantum computation. "But in terms of the evidence that they're solving problems using quantum mechanics faster than you could classically, I don't think it's there yet." A fierce critic of D-Wave in the years following its 2007 demo, Aaronson softened his stance last year after the company's Nature paper showing quantum effects. "In the past there was an enormous gap between the marketing claims and where the science was and that's come down, but there's still a gap," says Aaronson, who visited the company's labs in February. "The burden of proof is on them and they haven't met the burden yet."

Aaronson's biggest gripe is that the design of D-Wave's system could plausibly solve problems without quantum effects, in which case it would simply be a very weird conventional computer. He and other critics say the company must still prove two things: that its qubits really can enter superpositions and become entangled, and that the chip delivers a significant "quantum speed-up" compared to a classical computer working on the same problem. So far the company has presented proof of neither in a peer-reviewed forum.

If I had to wager today, my money would be on IBM.

Quantum cryptography: yesterday, today, and tomorrow

Chris Lee's impressive overview of quantum cryptography. Arstechnica, to my mind, does the best science reporting on quantum mechanics.

A real world example of the future of secure computation is found in the Danish sugar beet industry. All the sugar beets in Denmark are purchased by a single company. The farmers buy the rights to sell a certain volume of sugar beets to the monopolist. However, individual farmers must buy these rights based on estimates of their own production. As a result they often find themselves in the market to buy or sell rights.

Now, the last thing they want to do is buy and sell these rights through auctions run by the monopolist—monopoly power must be limited after all—because the monopolist would have the production records of every farmer and be able to use that to bid the price of the rights down. The market is setup by sellers simply listing the number of units they are willing to sell at each price. Buyers make a similar list of how many units they are willing buy at each price. The results are put together into two graphs of price and volume. Business is conducted at the intersection of these two curves.

Key to the success of this market is that no one knows who is in the market, or how much any particular farmer wants to buy or sell. A more open auction would reveal too much information, leaving farmers vulnerable to market manipulation by the monopolist and each other. So, secure computation could enable a way to create markets that are less open to manipulation, creating a fair economic mechanism.

Silicon Qubits

Well done video providing an overview of the research. Here is the original paper in Nature. For a more general explanation of the research, here is an article from The Register. See also the University of New South Wales's press release. Why is it that University press offices are loath to link to the original paper?

Quantum interpretations can make a difference

I stumbled upon this 2010 post by Chad Orzel talking about the many worlds interpretation to quantum mechanics. Chad has this to say about his general feelings towards the field of interpretations:

My real view is, alas, kind of wishy-washy: I’m agnostic about quantum interpretations, mostly because as far as we know, they’re all meta-theories, not proper scientific theories. There is no experimental test known that clearly favors one interpretation over another, so which one you like is ultimately a question of taste. They’re kind of fun to talk about, but absent a way to distinguish between them, they’re not more than that.

Matt Leifer has a great reply in the comments section:

You know, I couldn’t disagree more about this. In fact, I find it truly bizarre that quantum theory is pretty much the ONLY scientific theory where people do not think the the interpretation of the theory is an integral part of the theory itself. At least, I can’t think of any other examples.

Whilst it is true that an interpretation must reproduce the confirmed predictions of QM, they can differ quite a bit outside of that. The obvious example is spontaneous collapse theories, but there is also nonequilibrium Bohmian mechanics. Some may argue that these are different theories rather than different interpretations, but I think the dividing line between different theories and interpretations is rather blurry. It is not guaranteed that the interpretations will all agree when we are outside the realms of established physics, e.g. in quantum gravity.

The other thing that I think interpretations do for you is that they give different intuitions for how to proceed theoretically on certain problems. For example, the approach one takes to the emergence of classicality or to quantum chaos depends heavily on whether you view the state vector as an epistemic state (state of knowledge) or an ontic state (state of reality). This is one of the key issues that interpretations differ on.

In other words, interpretations CAN make a very real difference to how one does physics, and on controversial issues they probably SHOULD make a difference.

I like the way Matt puts this. Different interpretations provide different perspectives and approaches to a problem. I have found this to be true in my own work.

I still do not have a preferred interpretation, but that is because I know enough now to know that I still do not know enough to make an informed decision. There are to many nitty gritty subtleties that remain. I wish that someone would write a clear textbook on the subject. The quantum foundations version of Michael Nielsen's and Isaac Chuang's Quantum Computation and Quantum Information. I think such a text would help the field communicate and share with other branches of physics more effectively. I would certainly buy it. Is anyone working on such a project currently?

Explain quantum mechanics in five words

John Preskill, while talking about taking a quantum mechanics class with the late John Wheeler, mentions this story:

Later, at a student-faculty lunch, Wheeler seemed troubled. He had been asked to explain the essence of quantum mechanics in five words or less, and was stumped. Frank Calaprice, a nuclear physicist within earshot, interjected helpfully, “What we expect to measure?” I was silent.

The question was absurd. It was fascinating. I still think about it. I can’t answer it.

This idea–explain quantum mechanics in five words–has captured the imagination of people. In the the blog comments, a number of people chime in with their thoughts:

My attempt at non-technical answer is: Quantum mechanics is nature's casino.

Sean Carroll, via Michael Nielsen, picked up on the idea and posted this Twitter challenge:

Which has led to a flood of tweets trying to summarize quantum mechanics. Here are my favourites so far:

How would you explain quantum mechanics in five words or less?

The power of exponential growth and M&Ms

The power of exponential growth and M&Ms

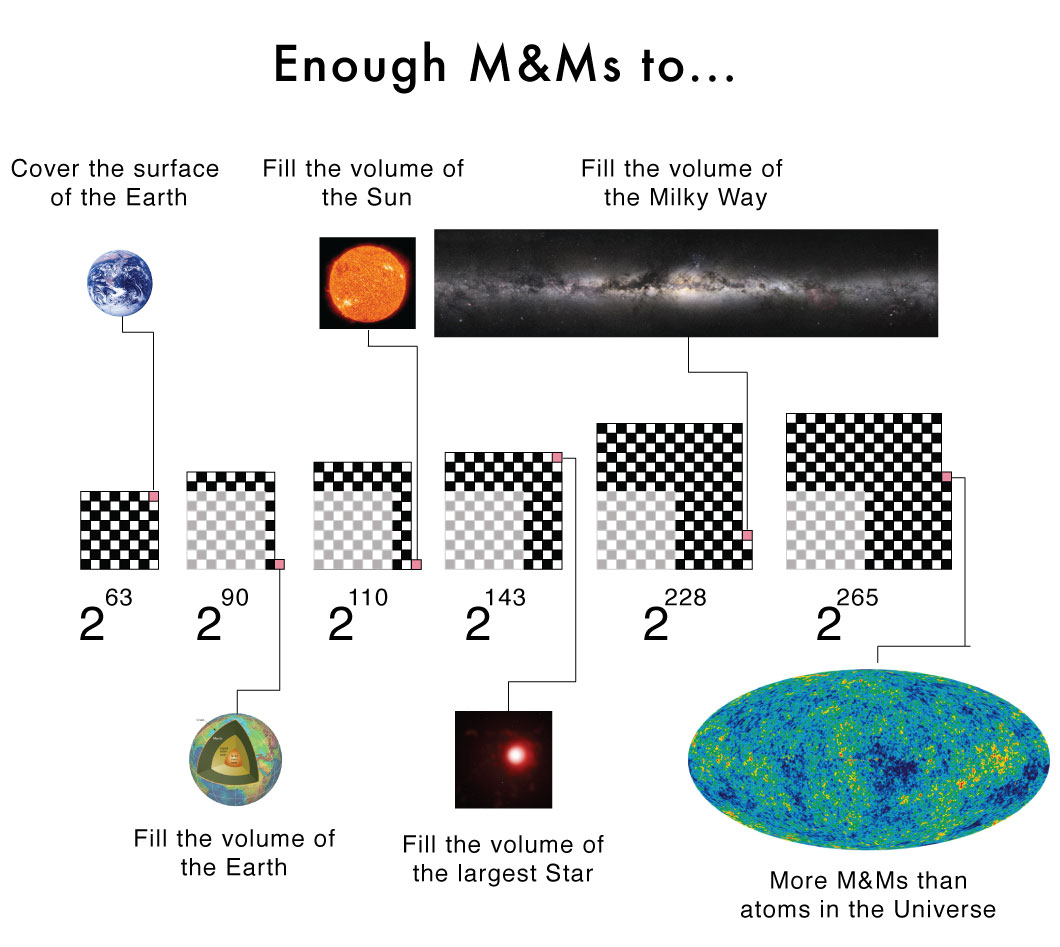
chess-boards-exponential-scaling.jpg

I made an error in my recent TEDxWaterloo talk. Inspired by the legend of Paal Paysam, I used a chessboard and a bowl of M&Ms to illustrate the power of exponential growth. On the first square of the chess board I placed a single M&M, then two on the second square, four on the third square, and so on doubling the number of M&Ms on each subsequent square. Continuing this way I would need 2^63 = 9,223,372,036,854,775,808 M&Ms1 to fill the 64th and final square. If each M&M is approximately 1cm^2 the last square would contain nearly enough M&Ms to cover the surface of the Earth, oceans included, twice over! TEDxWaterloo Krister with Smarties: Photo by Darin White of Makebright.com

But this is not what I said in my talk. I claimed you would need enough M&Ms to fill a bowl the size of the Earth (a volume). There is a big difference between surface area and a volume for a planet-sized object. If we assume2 each M&M is approximately 1 cm^3, then I was off by a factor of about 100 million3. Fortunately, this error does not weaken the argument I was making about the power of exponential growth. A factor of 100 million is large, but how many more times would we need to double the number of M&Ms in order to fill a bowl the size of the Earth? The answer is 27; instead of playing the doubling game on a chessboard with 64 squares we would instead need one with 91 squares. If we are going to add squares, why stop at 91? Here are some interesting numbers that we reach as we continue to add squares to our "super" chessboard.

Exponential scaling demonstrated with doubling periods, a chess board, and M&Ms

  • 111 squares (2^110): Enough M&Ms to fill a bowl the size of the Sun. They will melt pretty quickly.

  • 144 squares (2^143): This is enough M&M to fill a bowl the size of VY Canis Majoris, the largest known star with a radius 2200 times larger than the Sun.

  • 229 squares (2^228): Enough M&Ms to fill a bowl the size of the Milky Way, the galaxy not the chocolate bar, with M&Ms.

  • 266 squares (2^265): More M&Ms than there are atoms in the observable universe!. Various estimates put the number of atoms at ~10^80.

Exponential growth is powerful stuff!

  1. 64 doubling periods corresponds to 2^(64-1)=2^63 M&Ms. The first square contains 2^0=1 M&M. The second square has 2^1=4 M&Ms and so on. For N squares there will be 2^(N-1) M&Ms. ↩
  2. The volume of an M&M is roughly 0.636 cm^3 (see here or here). However, when packing M&M's into a bowl their will be some gaps between them. M&Ms can occupy a maximum of 68% of the volume in a bowl, leaving 32% empty. Therefore an M&M will occupy roughly 1 cm^3 (.636/.68). As a side note, you can fit more M&Ms into a bowl than perfect spheres. This was only discovered a few years ago, but has had a dramatic impact on many different fields. ↩
  3. I originally calculated the right answer (surface area), but before the talk only glanced over my old notes. I somehow got it stuck in my head that I was dealing with the Earth's volume instead of surface area. of course if we lived in the dark ages when the when the Earth was assumed to be flat, then my answer would be correct. ↩

The Quantum Dance

My TEDxWaterloo talk is out! With the help of a magician, a live band, and nearly 500 dancers from around the world, I explain how quantum entanglement can be used to build super fast computers. For more information on how the talk was put together check out the Project Q website.

Each part of the dance represents a different aspect of quantum computing. In the coming days I plan on writing a longer blog post that breaks down the routine and explains what is happening. Stay tuned.

QuTiP: Quantum Toolbox in Python

QuTiP: Quantum Toolbox in Python

jc_model_wigner_49.png

I was recently introduced to the quantum optics toolbox in Matlab, written by Sze Meng Tan, which is useful for quickly programming and studying a variety of quantum optics systems. Despite being great, the toolbox has not been updated since 2002.

Now there is QuTiP, a quantum toolbox for Python that is inspired by Sze's work. This software is actively maintained, and comes with a number of useful features. It is easy to parallelize certain tasks, it is more memory efficient, and it is faster. This toolbox has motivated me to learn Python–a surprisingly easy task. The excellent NumPy and Scipy libraries, along with Matplotlib, replicate most of the functionality found in Matlab with a similar syntax. A convenient way to install Python and the libraries that QuTip needs is to grab a copy of the Enthough Python Distribution, or if you already have Python installed to grab the Scipy Superpack. Note: QuTiP is only supported on Unix based systems like Linux or Mac OS X.

What makes this toolbox so great is that it allows you to write programs in a way that mimics how we write out physics problems. The program has lots of built in quantum opjects, such as annihilation, creation, squeezing, and displacement operators, that allow one to write down a Hamiltonian directly. Wigner and Q functions are built in, making it easy to plot quasi-probability distributions.

For example, this is the code used to create a coherent state.

N= 20 #Size of Hilbert Space 
alpha= 3 #amplitude of the coherent state 
D = displace(N,alpha) # Displacement operator 
vac= basis(N,0).unit() # Vacuum state 
psi=(D*vac).unit() # create a coherent state. The unit() ensures normalization.

It is easy to great operators as well. For example, let's look at how to create the nonstandard squeezing operator \(S3=\frac{1}{2}(\zeta^{\ast} a^{\dagger 3} - \zeta a^3),\) where \(\zeta\) is a squeezing parameter and \(a \) is the annihilation operator.

a = destroy(N) #annihilation operator 
S3=(1/2.0)*conj(zeta)*(a**3)-(1/2.0)*zeta*(a.dag())**3

Note: in Python ** means raise to the exponent. Here a**3 means \(a^3\).

QuTiP stores our operator as an object. One of the built-in methods allows us to exponentiate this operator so we can act on a state. For example, to create a squeezed state we act on the vacuum state with our squeezing operator, S3, and our displacement operator, D.

psi=(D*S3.expm()*vac).unit()

There is an impressive array of examples available from the QuTip website. The authors also have this paper that outlines how the program works, the performance benefits, and some excellent examples.

Here is a simple program I wrote, based on this example in the documentation, to plot the Wigner functions for a series of Schrödinger's cat states (a superposition of two different coherent states). The results are shown in the animated gif below.

# 3D Wigner functions for a series of cat states. #   
from qutip.states import *   
from qutip.Qobj import *   
from qutip.operators import *   
from qutip.wigner import *   
from mpl_toolkits.mplot3d import Axes3D   
from matplotlib import cm   
from pylab import *  

#setup constants: 
N = 20 # size of the Hilbert space 
alpha=linspace(0.01,3,60) # values for the coherent state amplitude 
a = destroy(N) #annihilation operator 
D = displace(N,alpha) # Displacement 
xvec = linspace(-9,9,300) 
X,Y = meshgrid(xvec, xvec)

k=1 # counter 
for x in alpha: 

    # Define the cat state. It is a coherent superposition of two coherent states. 
    # Each coherent state is created by the displacement operator acting on the vacuum. 
    # the unit() function makes sure that the overall state is normalized. 

    psi=(displace(N,x)*basis(N,0)-displace(N,-1*x)*basis(N,0)).unit();

    # plot the wigner function 
    W=wigner(psi,xvec,xvec) 
    fig =figure() 
    ax = Axes3D(fig,azim=-62.5,elev=25) 
    ax.plot_surface(X, Y, W, rstride=2, cstride=2, cmap=cm.jet,lw=.1) 
    ax.set_xlim3d(-9,9) 
    ax.set_xlim3d(-9,9) 
    ax.set_zlim3d(-.2,0.2) 
    ax.set_axis_off() 
    ax.set_frame_on('false') 
    title(r'$| \psi >= \frac{1}{\sqrt{2}}(|\alpha>-|-\alpha>)$'+r' $\alpha=$'+str(round(x,2))) 
    savefig("cat_state_"+str(k)+".png") k=k+1;
Wigner Functions of Schrödinger Cat State Animation

UPDATE: While I was writing this post, version 2 of QuTiP was released. I haven't had a chance to look at the new version in depth, but this looks like a solid update.

Project Q passes 300 participants

With a flurry of videos being submitted last night and today there are now 316 people who have taken part in Project Q! This is far beyond what I had hoped for. Thank you Lindy Hoppers for being so awesome.

Latest round of Project Q Submissions

We are up to 206 Lindy Hoppers who have taken part in Project Q! There have been a number of new cities who have submitted videos, and I know of a number of others who are either filming or working on their videos as the deadline approaches. I spent the past weekend working with the dancers, band, and other guests who will take part in the talk. It is going to be amazing. I cannot wait to show everyone the final product.

Project Q videos rolling in!

This past week there has been a flurry of activity with scenes around the world submitting their Project Q videos. So far 90 dancers from six cities have submitted videos! I know there are several more cities shooting their videos this weekend. I'll update the blog (and Project Q page) once the new submissions are online.

Here are some of the videos that have come in so far:

While I was in Vancouver last week I also filmed the local scene there performing the routine. I haven't had a chance to post it online, but will do so later on this weekend.

A big thanks to everyone who has helped out so far. I really appreciate it.

HELP: What is your favourite science poem?

Next Wednesday I am giving a lecture to a first-year poetry class on the "Physics of Poetry". In this talk I am going to discuss some of the connections between physics & poetry that I have encountered. I need some help though. Specifically, I would like to find out three things:

  1. Some examples of poems that discuss Science? (ie When I heard the Learn’d Astronomer).
  2. Has poetry influenced the way you see the world?
  3. As a scientist, has poetry influenced your work or the way you share your work?

Any suggestions, thoughts, or comments people have would be greatly appreciated!

George and John’s Excellent Adventures in Quantum Entanglement

A clever video by Scientific American about quantum entanglement and Bell's Theorem. This is one of the better attempts that I have seen to explain the concept of hidden variables and the surprising nature of Bell's inequalities.

I have thought long and hard about the best way to explain Bell's inequalities. I would still prefer a less abstract approach, but I really like the way this video introduces the subject and I can't think of anything better off the top of my head. Up to now I have used1 a different card trick to illustrate the surprising correlations that exist between entangled particles and not attempted to explain Bell's work. Perhaps I can convince Marco and Robert to reprise their roles as Einstein and Bohr in a sequel.

Entanglement is such an awesome phenomena that has ramifications in philosophy, physics, cosmology, and biology. Sometimes I take for granted that I get to create entangled states of light in the lab every day.

  1. Technically it is Dan Trommater, my magician friend, who performed the card trick. ↩