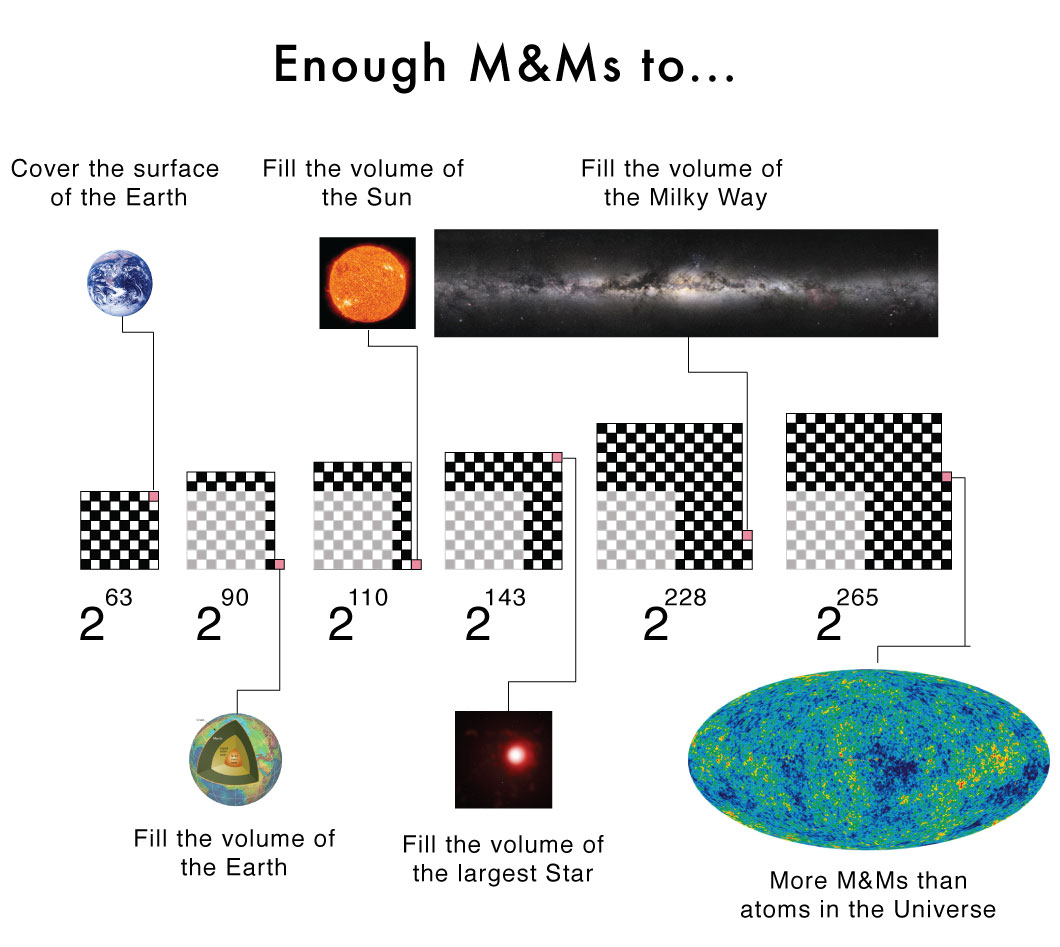
I made an error in my recent TEDxWaterloo talk. Inspired by the legend of Paal Paysam, I used a chessboard and a bowl of M&Ms to illustrate the power of exponential growth. On the first square of the chess board I placed a single M&M, then two on the second square, four on the third square, and so on doubling the number of M&Ms on each subsequent square. Continuing this way I would need 2^63 = 9,223,372,036,854,775,808 M&Ms1 to fill the 64th and final square. If each M&M is approximately 1cm^2 the last square would contain nearly enough M&Ms to cover the surface of the Earth, oceans included, twice over!

But this is not what I said in my talk. I claimed you would need enough M&Ms to fill a bowl the size of the Earth (a volume). There is a big difference between surface area and a volume for a planet-sized object. If we assume2 each M&M is approximately 1 cm^3, then I was off by a factor of about 100 million3. Fortunately, this error does not weaken the argument I was making about the power of exponential growth. A factor of 100 million is large, but how many more times would we need to double the number of M&Ms in order to fill a bowl the size of the Earth? The answer is 27; instead of playing the doubling game on a chessboard with 64 squares we would instead need one with 91 squares. If we are going to add squares, why stop at 91? Here are some interesting numbers that we reach as we continue to add squares to our "super" chessboard.
- 111 squares (2^110): Enough M&Ms to fill a bowl the size of the Sun. They will melt pretty quickly.
-
144 squares (2^143): This is enough M&M to fill a bowl the size of VY Canis Majoris, the largest known star with a radius 2200 times larger than the Sun.
-
229 squares (2^228): Enough M&Ms to fill a bowl the size of the Milky Way, the galaxy not the chocolate bar, with M&Ms.
-
266 squares (2^265): More M&Ms than there are atoms in the observable universe!. Various estimates put the number of atoms at ~10^80.
Exponential growth is powerful stuff!
- 64 doubling periods corresponds to 2^(64-1)=2^63 M&Ms. The first square contains 2^0=1 M&M. The second square has 2^1=4 M&Ms and so on. For N squares there will be 2^(N-1) M&Ms. ↩
- The volume of an M&M is roughly 0.636 cm^3 (see here or here). However, when packing M&M's into a bowl their will be some gaps between them. M&Ms can occupy a maximum of 68% of the volume in a bowl, leaving 32% empty. Therefore an M&M will occupy roughly 1 cm^3 (.636/.68). As a side note, you can fit more M&Ms into a bowl than perfect spheres. This was only discovered a few years ago, but has had a dramatic impact on many different fields. ↩
- I originally calculated the right answer (surface area), but before the talk only glanced over my old notes. I somehow got it stuck in my head that I was dealing with the Earth's volume instead of surface area. of course if we lived in the dark ages when the when the Earth was assumed to be flat, then my answer would be correct. ↩